Mastering multiplication tables from 1-12 opens the door to swift calculations and a strong foundation in mathematics.
In this article, we will provide you with a Multiplication Chart 12×12 PDF free printable and some handy tips and tricks that will make navigating the multiplication chart even easier.
Understanding the Multiplication Chart
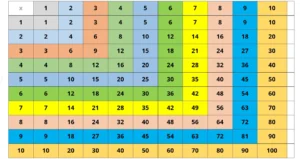
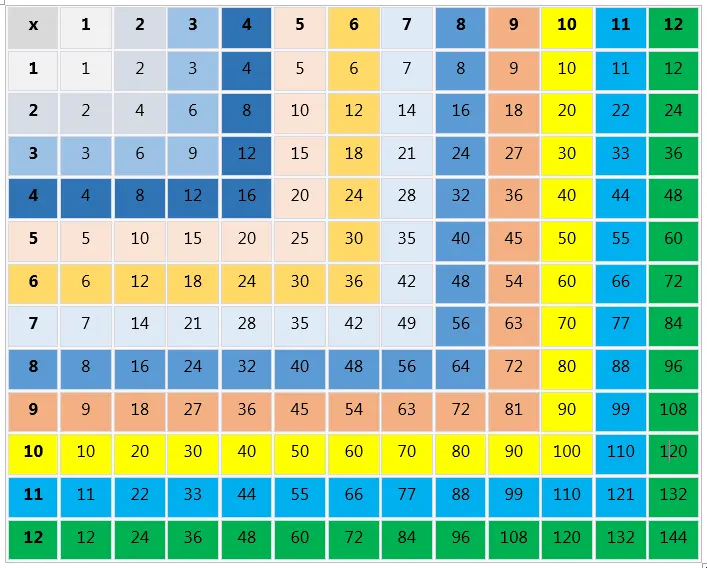
The multiplication chart, often referred to as the multiplication table, is a structured grid that showcases the outcomes of multiplying two numbers from 1 to 12.
At the crossroads of each row and column lies the product of the corresponding row number and column number.
Let’s take a closer look at how this chart works:
| x | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 2 | 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 | 20 | 22 | 24 |
| 3 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 | 27 | 30 | 33 | 36 |
| 4 | 4 | 8 | 12 | 16 | 20 | 24 | 28 | 32 | 36 | 40 | 44 | 48 |
| 5 | 5 | 10 | 15 | 20 | 25 | 30 | 35 | 40 | 45 | 50 | 55 | 60 |
| 6 | 6 | 12 | 18 | 24 | 30 | 36 | 42 | 48 | 54 | 60 | 66 | 72 |
| 7 | 7 | 14 | 21 | 28 | 35 | 42 | 49 | 56 | 63 | 70 | 77 | 84 |
| 8 | 8 | 16 | 24 | 32 | 40 | 48 | 56 | 64 | 72 | 80 | 88 | 96 |
| 9 | 9 | 18 | 27 | 36 | 45 | 54 | 63 | 72 | 81 | 90 | 99 | 108 |
| 10 | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 | 110 | 120 |
| 11 | 11 | 22 | 33 | 44 | 55 | 66 | 77 | 88 | 99 | 110 | 121 | 132 |
| 12 | 12 | 24 | 36 | 48 | 60 | 72 | 84 | 96 | 108 | 120 | 132 | 144 |
1. Multiplication Chart 1-12 Colored
2. Multiplication Chart 1-12 Blank

How to Read Multiplication Chart 1-12
- Row-wise Comprehension: To find the product of, say, 7 × 8, locate the row for 7 and the column for 8. The number at their intersection (56) is your answer.
- Multiplying by 1: Any number multiplied by 1 equals the number itself. This is evident from the diagonal line of 1s in the chart.
- Patterns and Insights: Observing the chart can reveal patterns like doubling (2 × 2 = 4, 4 × 2 = 8) and symmetry (3 × 4 = 4 × 3 = 12).
Tips and Tricks
Tip 1: Counting by Multiples
Counting by multiples is a neat trick to find products quickly. For example, to calculate 7 × 6, think of it as 7 × 5 (which is 35) and then add one more group of 7 (which is 7). So, 7 × 6 = 35 + 7 = 42.
Tip 2: Doubling and Halving
Doubling and halving are efficient strategies for multiplication. When you’re multiplying an even number by 2, simply double the number.
If you’re multiplying by 4, double the number twice. For example, 6 × 4 is the same as 6 × 2 × 2, which is 24.
Tip 3: The Power of 9
Multiplying by 9 can seem tricky, but there’s a pattern to exploit. Write down the digits 0 to 9. Now, when you multiply a number by 9, the digits in the product will add up to 9. For example, 9 × 6 = 54 (5 + 4 = 9).
Tip 4: Using 10 as a Helper
When multiplying by 10, the product is simply the number with a zero tacked on the end. This is a great way to introduce place value to young learners. For instance, 8 × 10 = 80.
Tip 5: Square Numbers
Squaring a number (multiplying it by itself) is another useful skill. For numbers 1 to 12, the squares follow a pattern: 1, 4, 9, 16, 25, 36, 49, 64, 81, 100, 121, and 144. This can be handy when you need to quickly find the square of a number.
Tip 6: Commutative Property
Remember that multiplication is commutative, meaning that switching the order of the factors doesn’t change the result. For example, 4 × 7 is the same as 7 × 4, and both equal 28.
Tip 7: Divide and Conquer
Division and multiplication are closely related. If you’re struggling to recall a multiplication fact, try dividing a known multiple of that number.
For instance, if you can’t remember 9 × 7, divide 63 (a known fact) by 9 to get 7.
Tip 8: Handy Patterns
Keep an eye out for number patterns. For example, the last digit of the product of any number multiplied by 5 will always be 0 or 5.
Tip 9: Using Friendly Numbers
Break down numbers into friendlier components. For 8 × 7, you could do (8 × 5) + (8 × 2), which is 40 + 16 = 56.
Tip 10: Mind the Zeros
When multiplying by 0, the product is always 0. It’s a simple rule, but it can be helpful to remember, especially when dealing with larger calculations.
Remember, practice makes perfect. The more you use these tips and tricks, the more confident you’ll become in mastering multiplication from 1 to 12.
See Also: Multiplication Chart 1-100 Free
Conclusion
Mastering multiplication from 1 to 12 is a valuable skill that streamlines calculations and enhances your mathematical prowess.
These tips and tricks offer insightful ways to approach multiplication and use the multiplication chart effectively.